2009年 大学入試センター試験 数学ⅡB 解説
第1問〔1〕 〔2〕 第2問 第3問 第4問
第2問
点
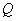
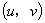 に関して点
に関して点
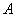 と対称な点を
と対称な点を
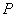 とすると,点
とすると,点
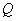 は点
は点
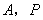 の中点となるので,
の中点となるので,
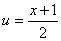 ,
,
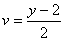 が成り立つ。
が成り立つ。
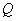 が
が
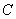 上を動く点
上を動く点
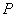 の軌跡を
の軌跡を
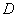 とすると,
とすると,
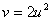 となるので
となるので
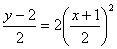
整理して
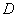 は放物線
は放物線
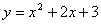 である。
である。
二つの放物線
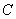 と
と
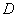 の交点
の交点
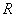 と
と
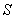 とする。
とする。
交点は,
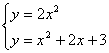 を連立させると,
を連立させると,
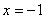 ,
,
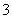
ただし,
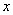 座標の小さい方を
座標の小さい方を
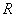 とする。点
とする。点
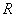 ,
,
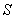 の
の
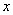 座標はそれぞれ
座標はそれぞれ
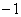 ,
,
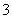 で,
で,
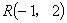 ,
,
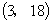
放物線
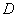 を
を
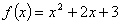 とすると,
とすると,
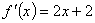 なので,
なので,
点
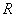 における放物線
における放物線
 の放物線は,
の放物線は,
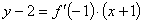
点
 における放物線
における放物線
 の放物線は,
の放物線は,
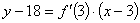
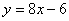
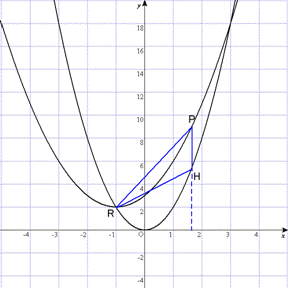
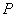 を放物線
を放物線
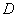 上の点とし,
上の点とし,
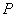 からの
からの
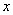 軸にひいた垂線と放物線
軸にひいた垂線と放物線
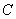 との交点を
との交点を
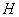 とする。
とする。
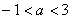 のとき,
のとき,
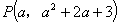 ,
,
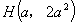 なので,
なので,
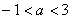 のとき,
のとき,
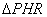 の面積
の面積
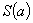 は,
は,
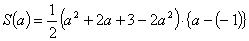
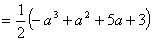
と表される。
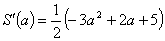
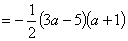
となり,増減表は
となり,
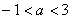 のとき,
のとき,
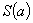 は
は
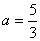 のとき最大値をとる。
のとき最大値をとる。
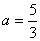 のとき,
のとき,
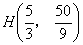 なので,直線
なので,直線
 は
は
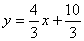
これと,
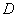 :
:
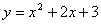 との交点を求めると,
との交点を求めると,
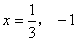
よって,直線
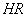 と放物線
と放物線
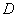 の交点のうち,
の交点のうち,
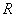 と異なる点の座標は
と異なる点の座標は
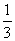 である。
である。
このとき,
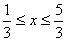 の範囲で,
の範囲で,
放物線
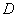 と直線
と直線
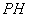 および直線
および直線
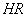 で囲まれた図形の面積は,
で囲まれた図形の面積は,
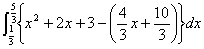
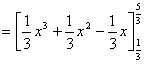
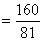
|


