2009年 大学入試センター試験 数学ⅡB 解説
第1問〔1〕 〔2〕 第2問 第3問 第4問
第4問
(1) ベクトルを成分で表すと,
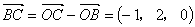
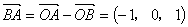
よって,
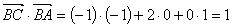
△
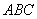 の面積は
の面積は
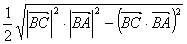 なので,
なので,
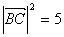 ,
,
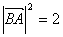 ,
,
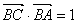 を代入して,
を代入して,
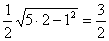
(2) 線分
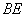 を考えると,
を考えると,
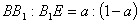 となるので,
となるので,
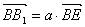
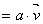 である。
である。
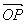 は
は
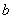 を用いて,
を用いて,
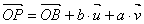 …①
…①
線分
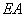 上の点
上の点
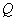 を考える。
を考える。
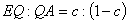 とおくと,
とおくと,

したがって,
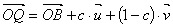 …②
…②
点
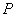 と点
と点
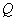 が一致するのは,①式と②式の係数を比較して考えればよい。
が一致するのは,①式と②式の係数を比較して考えればよい。
すなわち,
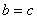 かつ
かつ
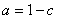 となれば良いので,
となれば良いので,
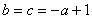 のとき点
のとき点
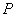 と点
と点
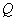 が一致する。
が一致する。
線分
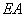 上の点
上の点
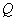 は
は
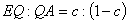 とおいて考えていたので,
とおいて考えていたので,
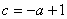 を利用して
を利用して
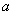 を用いて表すと,
を用いて表すと,
点
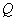 は
は
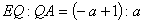 なので,
なので,
線分
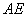 を
を
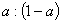 に内分する点で線分
に内分する点で線分
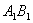 と交わることが分かります。
と交わることが分かります。
次に,
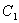 と
と
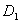 を考えます。
を考えます。
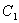 と
と
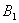 ,
,
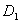 と
と
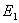 が対応するので,
が対応するので,
線分
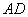 も
も
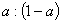 に内分する点で線分
に内分する点で線分
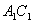 と交わることが分かります。
と交わることが分かります。
ここで,
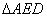 を抜き出すと,その中には相似比が
を抜き出すと,その中には相似比が
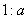 となる
となる
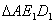 が存在するので,
が存在するので,
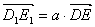 となります。
となります。
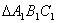 は
は
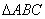 を平行移動させただけのものになるので,
を平行移動させただけのものになるので,
(1)より,
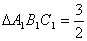
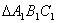 から相似比が
から相似比が
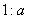 の
の
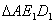 を除くと,四角形
を除くと,四角形
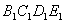 となるので,
となるので,
四角形
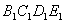 の面積は,
の面積は,
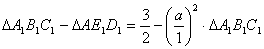
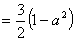
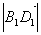 を求めるには
を求めるには
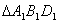 において,余弦定理を用います。
において,余弦定理を用います。
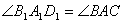 なので,
なので,
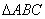 より
より
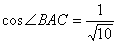 のとき,
のとき,
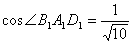
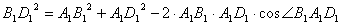
よって,
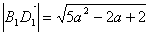
|


