|
|
 |
2010年 大学入試センター試験 数学ⅡB 解説
第1問〔1〕 〔2〕 第2問 第3問 第4問
(1)
 は第4群の最後の項を示すので,
は第4群の最後の項を示すので,
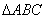
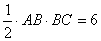
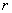
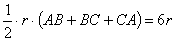 は第
は第
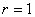 群の個数と一致するので,
群の個数と一致するので,
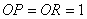
また,
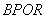
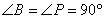 となる。
となる。
次に600を考える。
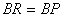 とすると,
とすると,
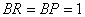
解の公式を利用して,
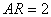
このとき,
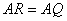 かつ
かつ
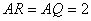 なので,
なので,

 のとき,
のとき,


となるので,600は第21群の10番目の項と分かる。
(2) 第
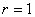 群の最後の項は,
群の最後の項は,
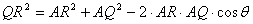 なので,第
なので,第
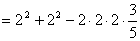 群の小さい方から
群の小さい方から
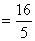 番目の項は,
番目の項は,
第
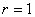 群の最後の項より
群の最後の項より
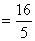 大きい数字なので,
大きい数字なので,
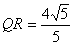
よって,
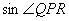
このことから
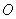
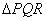
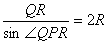
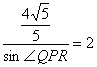
が成り立つ。
このことから,
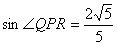
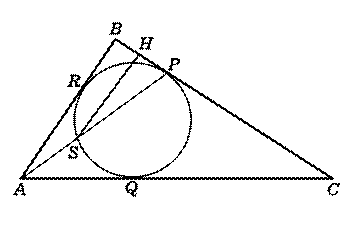
|
 |
|
|
 |
|
|
 |
|
|
 |
|
|
 |
|
|
 |
|
 |


