����
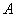 �ɑ��āC
�ɑ��āC
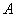 ���N����Ȃ��v�Ƃ������ۂ��C
���N����Ȃ��v�Ƃ������ۂ��C
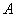 �̗]�����Ƃ����܂��B
�̗]�����Ƃ����܂��B
�L���ł́C
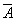 �ŕ\���܂��B���̍l�����͕�W���Ɠ����ł��B���̂Ƃ��ɁC
�ŕ\���܂��B���̍l�����͕�W���Ɠ����ł��B���̂Ƃ��ɁC
����
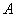 �Ǝ���
�Ǝ���
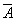 �͓����ɋN���邱�Ƃ͂��肦�܂���B���������āC�݂��ɔr���ɂȂ�܂��B
�͓����ɋN���邱�Ƃ͂��肦�܂���B���������āC�݂��ɔr���ɂȂ�܂��B
�܂��C���@�藝�ɂ��
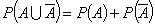
�ƂȂ�܂��B���̂Ƃ��ɁC���鎎�s�ɂ����Ď���
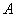 ���N����Ȃ��Ƃ��ɂ́C
���N����Ȃ��Ƃ��ɂ́C
�K������
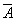 ���N����Ƃ��l���邱�Ƃ��o����̂ŁC
���N����Ƃ��l���邱�Ƃ��o����̂ŁC
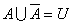
�ƍl���邱�Ƃ��o���܂��B���������āC
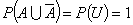
�ƂȂ�܂��B
���̂��Ƃ���C
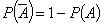
���wA�̖ڎ���
���w�̖ڎ��� |


