���
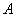 ��
��
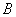 ���{�[�����O�������Ȃ��܂��B
���{�[�����O�������Ȃ��܂��B
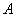 ��1���ڂŃX�g���C�N���o���m����
��1���ڂŃX�g���C�N���o���m����
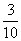 �ŁC
�ŁC
2���ڈȍ~��
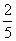 �ł��B�܂��C
�ł��B�܂��C
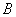 ��1���ڂŃX�g���C�N���o���m����
��1���ڂŃX�g���C�N���o���m����
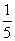 �ŁC
�ŁC
2���ڈȍ~��
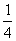 �ł��B
�ł��B
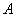 ��
��
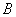 �����Ԃɓ�����Ƃ��ȉ��̖�ɓ�����B
�����Ԃɓ�����Ƃ��ȉ��̖�ɓ�����B
�������C�X�g���C�N���ǂ��炩���o�����Ƃ��Ƀ{�[�����O�͏I�����܂��B
�i�P�j�@
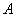 ���X�g���C�N��2���ڂ܂łɏo���m�������߂�B
���X�g���C�N��2���ڂ܂łɏo���m�������߂�B
�i�Q�j�@
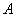 �C
�C
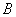 ���Ƃ���2���ڂ܂œ����I����Ă��X�g���C�N���o�Ȃ��m�������߂�B
���Ƃ���2���ڂ܂œ����I����Ă��X�g���C�N���o�Ȃ��m�������߂�B
���@��
�i�P�j�@
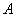 ��1���ڂɃX�g���C�N���o���m����
��1���ڂɃX�g���C�N���o���m����
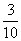
�@�@�@�@
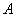 ��2���ڂɃX�g���C�N���o�����߂ɂ́C
��2���ڂɃX�g���C�N���o�����߂ɂ́C
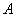 �C
�C
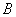 �͂Ƃ���1���ڂ̓X�g���C�N���o�����ɁC
�͂Ƃ���1���ڂ̓X�g���C�N���o�����ɁC
�@�@�@
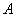 ��2���ڂɃX�g���C�N���o���悢�̂ŁC
��2���ڂɃX�g���C�N���o���悢�̂ŁC
�@�@�@�@
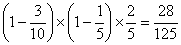
�@�@�@�@����āC
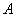 ��2���ڂ܂łɁC���Ȃ킿1���ڂ܂���2���ڂɃX�g���C�N���o���m���́C
��2���ڂ܂łɁC���Ȃ킿1���ڂ܂���2���ڂɃX�g���C�N���o���m���́C
�@�@�@�@
�i�Q�j�@
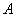 �C
�C
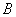 ���Ƃ���2���ڂ܂œ����I����Ă��X�g���C�N���o�Ȃ��m����
���Ƃ���2���ڂ܂œ����I����Ă��X�g���C�N���o�Ȃ��m����
�@�@�@�]���ۂ̊m���̐ςȂ̂ŁC
�@�@�@�@
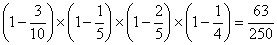
���wA�̖ڎ���
���w�̖ڎ��� |


